円順列とは
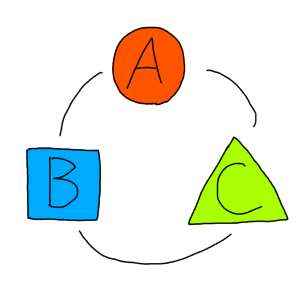
↑こうやって異なる物を円形に並べる順列のことです。
円形に並べるのが円順列で、一列に並べるのが順列。そして、円順列を理解するためにはまず順列がわかっていないといけません。
しかし、順列さえ分かっていれば円順列もすぐに理解できます。
そこでまずは一旦、おさらいの意味で普通の順列の計算方法から入りましょう。
順列の計算
A、B、Cの三人を一列に並べる場合を考えてみましょう。並べる場所をマスに例えて、以下のようなイラストを描いてみます。
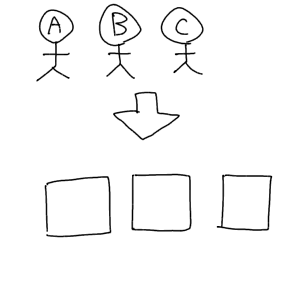
若干シュールな絵ができてしまいましたが、これが普通の順列です。この3人の並べるにあたって、まず左のマスから埋めていきましょう。
そうすると左のマスにはA、B、Cの3人いずれもが入りうるので、左のマスの埋め方は3通りあることになります。
そして左のマスに一人を埋めた結果、真ん中のマスに入れられる人は二人なので、真ん中のマスの埋め方は2通りあることになります。
そして最後、右のマスですが、この段階ではもう一人しか残っていないので、埋め方は1通りです。
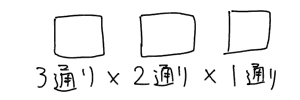
よって計算は
$_3P_3=3!=3\cdot 2\cdot 1=6$通り
となります。これが普通の順列。
そして円順列とは、この普通の順列で並べたマスをさらに円形にしたものです。
順列→円順列
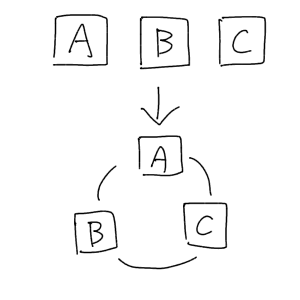
こういう感じで、もともと一列だったものを円形に並べ直すんです。
ちょっと見やすくするために色分けをしてみます。

それでですね、ここからが肝心の話なのですが、これは円形なので、回転させることができるんですね。こんな感じで↓
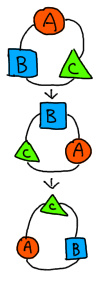
つまり、これら3つの円は回転させると同じものになるので、同一の円順列とみなすべきなんです。上の3つの回転形は、合わせて1つの円順列なんです。なので数え方は1通り。これが普通の順列と円順列の違いです。
普通の順列であれば、ABC、BCA、CABの3通りあったはずの数え方が、円順列では1通りになるんです。場合の数としては3分の1に減ったわけですね。
なので、さきほど計算した普通の順列の数$=6$通りは、円順列にすると$6\div 3=2$通りになるんです。
式で表すと
$\displaystyle\frac{_3P_3}{3}=\displaystyle\frac{3!}{3}=\displaystyle\frac{3\cdot 2\cdot 1}{3}=2$通り
これが円順列の計算方法です。より一般化した公式は
$\displaystyle\frac{_nP_n}{n}=\displaystyle\frac{n!}{n}=(n-1)!$
です。上の「三人を円形に並べる」の例でいうと$n=3$だったわけです。
円順列の計算は、このように普通の順列の式を個数で割ればいいんです。それが円順列の場合の数として求まります。
それでは確認として例題を解いてみましょう。
円順列の問題
問題
これはもう公式に当てはめるだけで即求まりますね。
6個の順列の式を6で割ればいいんです。
$\displaystyle\frac{_6P_6}{6}=\displaystyle\frac{6!}{6}=5!=5\cdot 4\cdot 3\cdot 2\cdot 1=120$通り
これで完成!円順列はこれでマスター!
……と言いたいところですが、円順列にはもう一つ似たような応用例があります。じゅず順列というものです。
円順列とじゅず(数珠)順列の違い
これは一度問題を解いてからのほうが説明がわかりやすいと思います。さっそく問題を解いてみましょう。
問題
ひとまずは円順列なので、そのまま計算してみます。
$\displaystyle\frac{_6P_6}{6}=\displaystyle\frac{6!}{6}=5!=5\cdot 4\cdot 3\cdot 2\cdot 1=120$通り
さきほどの問題と同じ答えが求まりました。しかし、さきほどはテーブルの上に並べたのに対し、今度は首飾りです。どう違うのでしょうか?
それは裏返しのパターンがあるということです。
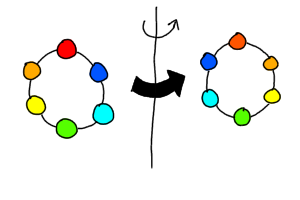
この2つの首飾りは裏返せば同じものになるので、1つのじゅず(数珠)順列として数えられます。円順列としては2通りですが、じゅず順列としては1通りなんです。これが円順列とじゅず順列の違いです。
なので計算としては、円順列の式を2で割ればいいんです。裏と表の2パターンなので2なんですね。
$\displaystyle\frac{_6P_6}{6\cdot 2}=\displaystyle\frac{6!}{6\cdot 2}=\displaystyle\frac{5!}{2}=\displaystyle\frac{5\cdot 4\cdot 3\cdot 2\cdot 1}{2}=\displaystyle\frac{120}{2}=60$通り
これがじゅず順列の答えです。
円順列とじゅず順列、見分け方は「裏返せるかどうか?」で判断すればよいです。
テーブルは裏返せないので円順列、首飾りは裏返せるのでじゅず順列、という見分け方です。テーブルはさすがに裏返せないですよね。裏返すと大変なことになりますから。
こんな感じで見分けると良いです。